Dr. Nganguia’s earliest involvement in research dates back to his undergraduate studies. In his sophomore year he began learning about ways mathematics could be used to model various processes and natural phenomena. He was introduced to fluid dynamics, and later co-authored his first paper investigating the plausible links between coastal topology and whale strandings.
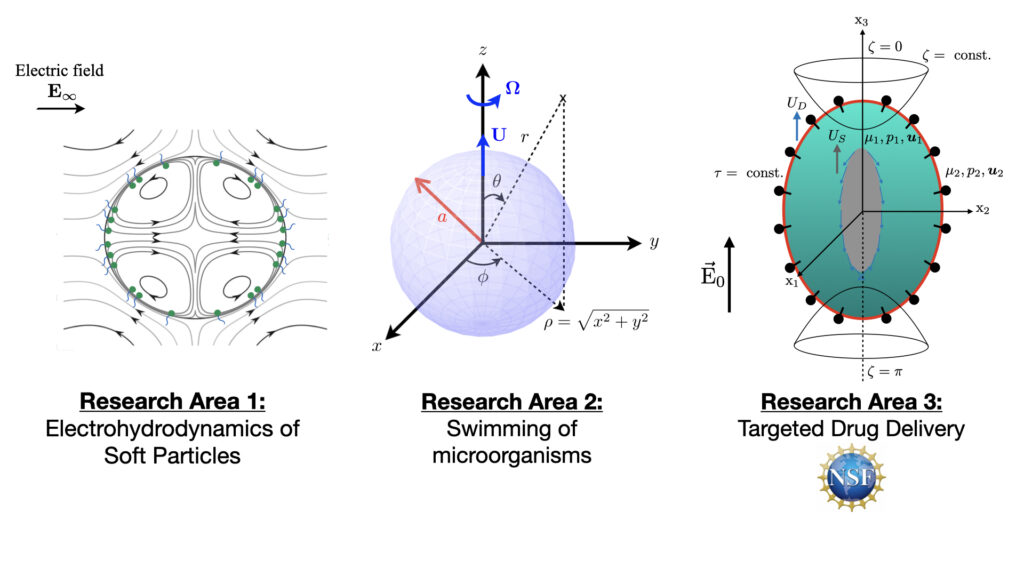
In graduate school, Dr. Nganguia turned his focus to applications in medicine and physiology. He wrote his doctoral dissertation on the response of deformable interfaces to an externally applied electric field, and pursued this research topic during his first postdoctoral appointment. In particular he considered how droplets (simple boundaries defined by surface tension), and vesicles (closed lipid layers frequently used as models for biological cells) deform when subjected to an electric field.
Later during his second postdoctoral appointment, Dr. Nganguia branched out and began investigating microorganisms’ swimming in complex fluids. He quickly found the topic practically relevant and nontrivial, considering microorganisms live in a world with negligible inertia (a world where viscous forces dominate). Moreover, while propulsion in simple fluids has enjoyed decades of productive research, microorganisms live in biological fluids that are heterogeneous and/or polymeric, displaying complex rheological properties. With this realization, Dr. Nganguia went on to study the swimming mechanics of microorganisms in so-called thin-shearing fluids, and in heterogeneous environments.
Dr. Nganguia is now working on integrating these theories (electrohydrodynamics and microorganisms’ propulsion) to investigate problems of practical relevance. Funded by the U.S. National Science Foundation, he hopes his research will help develop electrically-driven systems that can be deployed to improve patients’ care and outcomes. He continues to collaborate with colleagues at various institutions on these and other research projects related to mathematical biology and fluid dynamics.
Dr. Nganguia’s Mathematical Fluid Dynamics Group is recruiting students at both graduate and undergraduate levels. If you are interested in Mathematical Biology, Mathematical Physics, and/or multiscale modeling, and would like to join our group, please do not hesitate to contact me via email.
Graduate Students
- Ummul Aymen (2022-present): Applied Mathematics
- James Della-Giustina (2022-present): Applied Mathematics
- Omar Farooqui (2022-present): Applied Mathematics
Undergraduate Students
- Adedoyin “Doyin” Adegbuyi (2022-present): Computer Sciences/Mathematics
- Youssef Ben Bella (2022-present): Computer Sciences
- William “Will” Hunter (2022-present): Mathematics
- Ifenyinwa “Ife” Okeke (2022-present): Molecular Biology
Gallery
Fluids Group Announcements and Updates
- March 7-8, 2023: Aymen and James presented their research findings at the American Physical Society (APS) Meeting in Las Vegas
- February 9, 2023: Aymen, PI Nganguia and collaborators submitted a research paper for peer-review.
- December 22, 2022: PI Nganguia’s paper, titled “Influence of surface viscosities on the electrodeformation of a prolate viscous drop,” has been accepted for publication in Soft Matter (2021 IF: 4.046)
- December 20, 2022: Aymen successfully defended her graduate project. Congratulations, Aymen!
- November 2022: The group acquired two (2) M1-MAX Mac Studio, 10TB of external storage space, and other accessories to support its deep learning and numerical simulations. This acquisition is made possible through PI Nganguia’s Fischer Endowed Chair.
- November 2022: One member (Youssef) left the group while a new member, Doyin joined. Welcome Doyin!
- September 30, 2022: PI Nganguia and collaborators submitted a research paper for peer-review.
- August 31, 2022: The group held its inaugural meeting. Welcome to our graduate students: Aymen, James, and Omar, and our undergraduate students: Youssef, William, and Ife. PI Nganguia gratefully acknowledges support from the National Science Foundation (NSF) and from the Fischer Endowed Chair from TU’s Fischer College of Science and Mathematics (FCSM). Two graduate students (Aymen and James) and the undergraduate students are supported through NSF.